L’argomento è molto vasto ed affascinante e tira in ballo un pò di ambiti scientifici vari.
Per capire queste nozioni (almeno da un punto di vista non molto tecnico) non c’è bisogno che siate esperti di fisica e/o di ingegneria,
o esperti di acustica, ma solo che siate un po avvezzi alle scienze in generale; infatti di seguito farò riferimento all’elettronica,
alla fisica delle onde , all’ingegneria del suono e naturalmente alla matematica (che farà da sfondo), vi prego di perdonarmi se qualche volta mi lascerò
andare ed entrerò nei tecnicismi, ma è più forte di me… tuttavia cercherò di essere il più chiaro possibile ;).
$$ \diamond\diamond\diamond $$
La fisica di un suono
Un suono si può definire in un modo molto semplice: è sostanzialmente un passaggio di forze in un mezzo, come ad esempio l’aria o l’acqua. Per capire quest’affermazione condurremo un esperimento. Consideriamo un diapason. Un diapason è un oggetto metallico a forma di \( Y\), che, se colpito emette un tono puro, cioè una nota ben precisa ad esempio un \( LA\). Ora la domanda è. Cosa accade quando il diapason viene percosso? E cosa percepiamo con il nostro orecchio?
La cosa è molto semplice: quando colpiamo il diapason, esso inizia a vibrare per via della sua elasticità, questa vibrazione è trasmessa alle particelle d’aria le quali risentono della vibrazione e la propagano alle particelle vicine (questo è il passaggio di forze), naturalmente quando le particelle si spostano si creano due fenomeni connessi: una pressione ed una depressione nel mezzo. Questi due fenomeni si propagano ad una certa velocità ed inoltre si ripetono periodicamente. In questo modo si definiscono due grandezze: la velocità del suono relativa al mezzo e la frequenza di oscillazione, la prima si misura in \( {m \over s}\), la seconda in \( Hz \).
If you want to live a happy life, tie it to a goal, not to people or things
Albert einstein
Un suono si comporta come un’onda e per questo la descrizione
matematica fa uso delle funzioni trigonometriche elementari seno e coseno. In generale si introduce una funzione speciale detta
armonica elementare o tono. L’equazione di un’armonica elementare è
$$ \mathrm A_0 sin(\omega t + \phi) $$
dove: \( A_0 \) è L’ampiezza del segnale, \( \omega\) è la pulsazione,
\( \phi \) è la fase e \( t\) è il tempo. Naturalmente nella formula sono
“nascosti” anche frequenza e periodo, valgono infatti le seguenti relazioni:
$$ f = {\omega \over 2\pi} \hspace{1cm} \omega = 2\pi f \hspace{1cm} f = {1 \over \mathrm T} $$
Cerchiamo di fare un po di chiarezza su queste grandezze,
prima di entrare nel vivo della trattazione: \( t\) è il tempo e su questo non mi dilungo più di tanto,
naturalmente si misura in secondi \((s)\). L’ampiezza misura quanto è intensa l’onda, quello che brutalmente chiamiamo
“il volume”, in realtà sarebbe l’intensità o altezza dell’onda (da non confondere con l’altezza nel senso musicale)
che si misura in metri \((m)\). \( \omega\) è la pulsazione. La pulsazione è una misura della velocità angolare
quando l’armonica rappresenta il moto di un punto su un cerchio, per questo le funzioni trigonometriche sono note
anche con il termine funzioni circolari, (tuttavia non c’è bisogno di sapere molto sulla pulsazione,
se non che si misura in \(({rad \over s}))\), e che \( f = {\omega \over 2\pi} \) – la cosa fondamentale è
che essa è correlata alla frequenza, dalle relazioni in alto. La frequenza misura il numero di
oscillazioni dell’onda in un intervallo di tempo finito (se l’intervallo è pari ad ( 1s)) si misura in \((Hz = s^{-1})\).
Infine il periodo \( \mathrm T\) che si misura in \( (s)\) è il tempo per compiere un’intera oscillazione.
Rimane una grandezza importante: la lunghezza d’onda ( \lambda) (in metri) che è correlata alle altre
grandezze dalla seguente relazione: \( \lambda = {v \over f} \). Facendo i dovuti calcoli, si scopre che il suono viaggia
più velocemente nei mezzi solidi e più lentamente nei mezzi gassosi: \( v_{s_{ACCIAIO}} = 5900 {m\over s}), ( v_{s_{ACQUA}} = 1484{m \over s}), ( v_{s_{ARIA}} = 343 {m \over s}\))
$$ \diamond\diamond\diamond $$
Analisi armonica di Fourier
Uno dei risultati più straordinari mai raggiunti dall’uomo è senz’altro l’analisi di Fourier o Analisi Armonica. Di che si tratta? in sostanza, tutto si fonda su una teoria, scoperta e sviluppata nei primi anni dell’ 800 da
Joseph Baptiste Fourier durante i suoi studi sulla trasmissione del calore. Egli scopri una cosa assolutamente stupefacente mentre era alle prese con le formule della fisica del calore.
Quello che scoprì è questo. Se prendiamo un’ onda complessa (non pura), come ad esempio quella prodotta da uno strumento musicale,
essa la si può scomporre come una somma infinita di toni puri (o armoniche elementari)! Un fatto straordinario! E come se voi stesse smontando un puzzle fino a
giungere alle singole tessere. Quando le tessere sono messe insieme si udisce l’intera armonia, ma prese singolarmente esse sono dei suoni elementari costituiti da una sola nota.
L’esempio tipico è quello di una corda che viene pizzicata, quello che accade e che essa inizia a vibrare, anzitutto alla sua frequenza fondamentale, ma non solo essa vibrerà ad una frequenza doppia ,
tripla, multipla ecc… si parla di armoniche superiori (è l’insieme di queste armoniche costituisce il timbro caratteristico di quella corda specifica). La serie di Fourier
rappresenta un segnale come combinazione di armoniche elementari le cui ampiezze sono espresse dai cosiddetti coefficienti di Fourier:
$$ \small x(t) = {a_0 \over 2} + \sum_{j=1}^\infty \alpha(t)cos(\omega t) + \beta(t) sin(\omega t) $$
$$ \alpha_0 = {2\over \pi}\int_{-\pi}^{\pi}f(\xi)d\xi $$ $$\alpha_k = {1\over \pi}\int_{-\pi}^{\pi}f(\xi)cos(k\xi)d\xi $$ $$ \beta_k = {1\over \pi}\int_{-\pi}^{\pi}f(\xi)sin(k\xi)d\xi $$
Questa formula, avrete notato, vale solo per funzioni periodiche come le funzioni trigonometriche elementari.
Ma cosa accade se un segnale non è periodico? Fortunatamente esiste un altro oggetto dalle mille sfaccettature, la cosiddetta
Trasformata di Fourier che è la versione integrale “(super-potente)” della più semplice serie.
$$ X(f) = \int_{-\infty}^{+\infty} X(t) e^{-j\omega t} dt $$
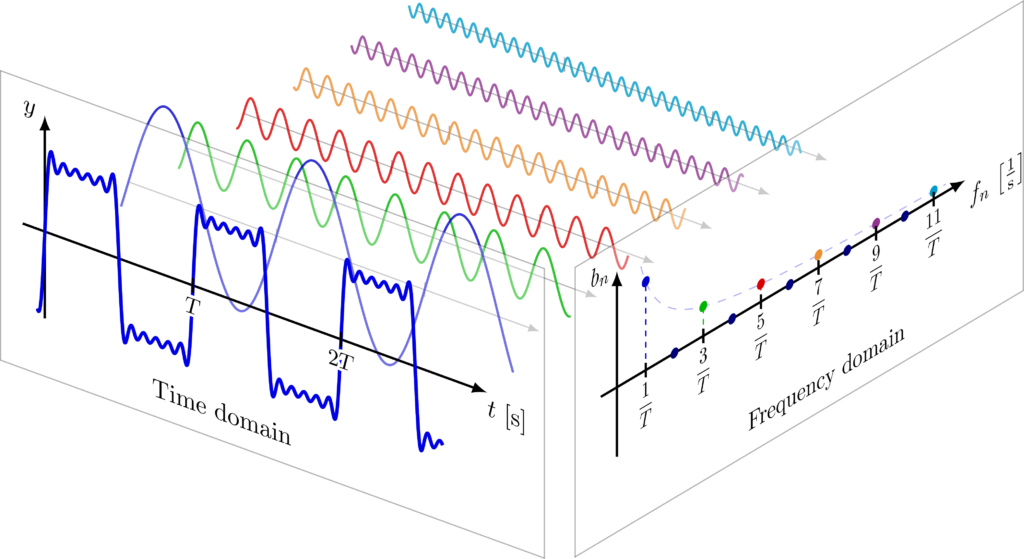
Queste due formule sono alla base di tutta la teoria delle onde e dei principi che governano il
campionamento e la trattazione dei segnali, soprattutto la trasformata. Essa trova impiego nei contesti più disparati,
dall’analisi delle immagini, alla trattazione dei segnali per non parlare di tutti i contesti legati alla medicina nucleare e alla fisica. E’ uno strumento assolutamente fondamentale.
$$ \diamond\diamond\diamond $$
Trasduttori e induzione elettromagnetica
Con il termine trasduttore, ci si riferisce ad una classe di dispoditivi elettromeccanici,
comunemente noti come diffusori o (altoparlanti) e microfoni. I primi trasformano un segnale elettrico in un moto vibrante
(meccanico) e quindi ri-producono i suoni, i secondi fanno il contrario: trasformano i suoni in segnali elettrici. La cosa sorprendente è che fisicamente
il principio è lo stesso e si basa sulla terza equazione di Maxwell, ossia la legge dell’induzione di Faraday-Lenz.
$$ \nabla \times \mathrm E = -{\partial \mathrm B \over \partial t} $$
Questa equazione racchiude tutto! Non solo questioni legate ai suoni, ma tutto ciò che è inerente all’elettromagnetismo in generale.
Quindi correnti alternate, motori, dinamo, induzioni, trasformatori ed una marea di altri fenomeni. Quindi è importante che ne capiate i
fondamenti Vediamo di capire quali sono gli oggetti che compaiono in essa.
- \( \mathrm E \) è il campo elettrico.
- \( -{\partial \mathrm B \over \partial t}\) è la derivata parziale del campo magnetico nel tempo.
- \( \nabla \times \) è l’operatore rotore che agisce nello spazio e calcola le rotazioni locali di un campo.
Sostanzialmente, l’equazione ci dice una cosa sorprendente! Quando c’è una variazione di campo magnetico nel tempo: \( -{\partial \mathrm B \over \partial t}\) (ad esempio se sposto un magnete), allora si genera un campo elettrico nello spazio! E viceversa. Questo fenomeno si chiama induzione elettromagnetica ed è alla base della fisica dei trasduttori. Fatte queste premesse vediamo ora cosa accade ad un suono quando incontra un microfono.
$$ \diamond\diamond\diamond $$
Il microfono elettrodinamico
Un microfono elettrodinamico è un apparecchio elettromeccanico costituito tre elementi fondamentali: una bobina, un
magnete ed una membrana. La bobina è ancorata alla membrana, di modo che il suo movimento le viene trasferito direttamente.
Il magnete, di solito di forma cilindrica, è ancorato nella bobina come in figura:

Quando un suono investe un microfono, la membrana inizia a vibrare alla stessa frequenza del suono.
Anche la bobina inizia a vibrare alla stessa frequenza del suono, ed è quì che entra in scena l’induzione elettromagnetica!
Siccome il magnete è fisso e la bobina è in movimento, c’è una variazione di campo magnetico, che produce un campo elettrico
nello spazio, il quale genera una corrente indotta nella bobina. Questa corrente è il nostro segnale acustico convertito in segnale elettrico. E voilà!
Il microfono elettrodinamico
Quando un segnale elettrico giunge ai capi di un diffusore, succede un fenomeno inverso.
Solo che ora il segnale non è più generato come in precedenza, ma percorre la bobina dell’altoparlante –
in questo modo si genera un campo magnetico il quale provoca la vibrazione della membrana. Subentra un piccolo problema: la
risonanza. Sapete cos’è la risonanza? E’ quando ad esempio due oggetti si mettono a vibrare in fase.
Prendete due diapason colpite il primo ed avvicinatelo al secondo, vedrete che essi si accorderanno
alla medesima vibrazione (entreranno in risonanza). Ogni oggetto possiede la sua frequenza di risonanza caratteristica.
Essa è la frequenza per cui le particelle del materiale si accordano e vibrano, l’intera struttura di questo oggetto vibra
ed entra in risonanza con il tono. Questo fatto provoca disturbi e molto spesso porta alla rottura della struttura stessa,
non per questo la risonanza è impiegata per distruggere! :).
$$ \diamond\diamond\diamond $$
Risonanza, filtri e risposta in frequenza
Risuonatori di Helmoltz
L’esempio più semplice di cavità risonante è il cosiddetto risuonatore di Helmoltz. Un RdH è sostanzialmente una sfera con un foro. Non so se vi è capitato qualche volta di soffiare sul collo di una bottiglia e provocare una sorta di fischio… ebbene, avete fatto risuonare la bottiglia secondo il principio del risuonatore. Infatti ogni bottiglia è una cavità risonante con la propria frequenza di risonanza di Helmoltz. E’ possibile calcolar tale frequenza attraverso la seguente formula:
$$ f_{0} = {1 \over 2\pi} \sqrt{S \over lV} = {1 \over 2\pi}\sqrt{S\over l+{\pi r\over 2}}$$
Logaritmi e decibels
Quando parliamo di segnali, di solito operiamo su domini molto estesi. In questi casi la soluzione ci viene dal concetto di decibel il quale è strettamente connesso al concetto di logaritmo. Il logaritmo deriva dall’algebra elementare e rappresenta l’esponente da mettere ad una base per ottenere un certo valore incognito. Detto in altri termini: dato un calore \(c\) ed una base \( b\), qual è l’esponente \( x\) da mettere a \(b\) per ottenere \( c\): \( b^x = c\)? Ad esempio qual è il logaritmo (in base 2 di 16), la risposta è 4, tutto questo si scrive come: \( log_2(16) = 4 \), perché \( 2^4 = 16 \). perfetto! Siccome avete capito, provate a calcolare: \(log_3(1) \), \(log_10(10) \) e \(log_2(0) \) . Ma vediamo ora cos’è il decibel:
Consideriamo una grandezza \( {\large X} \) che può rappresentare ad esempio un’intensità sonora, un livello di segnale di tensione, l’intensità luminosa di un fascio di fotoni ecc.. Vogliamo misurare questa grandezza ed esprimerla in db. Per fare questo, siccome ciò che misuriamo è una quantità relativa in correlazione ad un valore di riferimento, bisogna scegliere questo valore di riferimento \( {\large X_0} \) in base al quale la formula del decibel (in basso), trasforma la quantità \( {\large X} \) in db. $$ {\Large X_{db} \overset{{\small def}}{=} 10 \cdot log \left\lVert \frac{X}{X_0} \right\rVert } $$ Una misura in decibel si esprime come il logaritmo del valore assoluto del rapporto tra la grandezza originale ed una grandezza presa come riferimento o (taratura). Quindi il decibel non è altro che una misura relativa.
Diagrammi di Bode e risposta in frequenza
Dalla teoria dei controlli automatici, possiamo costruire un modello dinamico di un qualsiasi apparecchio elettronico come ad esempio un trasduttore. Possiamo descrivere il tutto da due punti di vista differenti. Il dominio del tempo ed il dominio della frequenza. Per ogni modello dinamico esisite uno strumento rappresentativo che ne caratterizza la cosiddetta risposta all’impulso, ossia la funzione di trasferimento, quando esprimo la funzione di trasferimento nel dominio della frequenza \(G(j\omega)\) ottengo la risposta in frequenza relativa al modello. La risposta in frequenza, analizza il comportamento del modello rispetto allo spettro delle frequenza e ne descrive il comportamento come filtro, ossia se esso attenua o amplifica determinate bande di frequenza. La \( G(j\omega) \) è un numero complesso e per esso e possibile studiarne modulo ed argomento, i due grafici costituiscono i diagrammi di Bode
La caratteristica di questi diagrammi sta nel fatto che essi sono logaritmici e non lineari. Il motivo è che una scala logaritmica, rispetto ad una lineare ha la proprietà di dilatazione e compressione. La dilatazione avviene da \( 0\) ad \(1\), mentre la compressione da \(1\) a \( +\infty\)
Analizziamo brevemente i due diagrammi. Anzitutto in entrambi, l’ascissa riporta il valore della frequenza in Hertz \( Hz\). Il diagramma dei moduli riporta in ordinata il valore del modulo della risposta in frequenza in decibel \( |G(j\omega)|_{dB}\), mentre il diagramma delle fasi riporta la fase in radianti \( \angle{G(j\omega)}_{rad}\)


Filtri
Ogni modello può essere un filtro. Cioè, qualsiasi componente meccanico o elettronico, o di altro genere. La risposta in frequenza, è la restrizione sull’asse immaginario della funzione di trasferimento. In base ad essa possiamo studiare il comportamento di un modello al variare della frequenza. Per semplicità consideriamo un trasduttore. La risposta in frequenza di un trasduttore, ad esempio un altoparlante, mi da informazioni su come esso riproduce lo spettro delle frequenze, mentre un microfono come assorbe lo spettro delle frequenze.
Saper leggere un diagramma di Bode è interessante per apprezzare i pregi ed i difetti di un apparecchio, ad esempio qual è la sua frequenza di risonanza, oppure qual è la sua impedenza intrinseca oppure come esso si comporta in relazione ad alcuni tipi di segnali: impulsi di Dirac, funzioni di Heaviside e treni di impulsi ma qui ci stiamo dilungando un po troppo. In ambito acustico, i filtri (passivi) vengono costruiti ad hoc attraverso componenti elettronici elementari, come ad esempio induttori, condensatori, e resistori, per realizzare apparecchi per il controllo della banda delle frequenze, questi apparecchi sono comunemente noti con il termine: passa basso, passa alto, passa banda, notch e sono raffigurati di seguito, assieme agli schemi circuitali.




Ci sarebbe tanto da discutere su questo, ma credo che in questa breve introduzione non è il momento di entrare nei dettagli tecnici, lo farò poi successivamente.
Diagrammi polari
I diagrammi polari, misurano l’attenuazione “circosferica” delle capsule microfoniche, detto brutalmente: qual è il livello di percezione del microfono nello spazio. Esistono circa sei diagrammi polari, che riprendono il nome dalla geometria delle curve polari nel piano complesso. Di seguito riporto un paio di esempi di diagrammi con relative parametrizzazioni delle funzioni.
$$ \diamond\diamond\diamond $$
Risonanza, filtri e risposta in frequenza
Finora abbiamo studiato un suono nel dominio del tempo e della frequenza in ambito analogico,
ma come possiamo dimenticarci dell’altra faccia della medaglia, ossia il mondo digitale? Vivendo in un era altamente tecnologica,
dove il computer regna sovrano, sarebbe un sacrilegio non parlarne…
Vediamo in primis qual è la differenza tra un segnale analogico ed un segnale digitale.
Un segnale analogico rappresenta una grandezza “pura” nel senso che l’informazione del segnale, racchiude tutti i valori possibili in modo continuo.
Un segnale digitale, viceversa è una versione discreta (approssimata) di un segnale analogico. In questo caso vi è una perdita di informazione del segnale.
Subentra il problema di trasformare un segnale da analogico in digitale e viceversa. Domanda, secondo voi quale dei due processi è più complesso ADC o DCA? Vi lascio con questa domanda in sospeso… sarò lieto di ricevere qualche vostro feedback ;). Quando si deve trasformare un segnale analogico in uno digitale, bisogna effettuare diverse fasi: il campionamento, la quantizzazione e la codifica. La fase più importante di tutte è sicuramente la prima. In questa fase, il segnale analogico viene misurato ad intervalli discreti di tempo ad una certa velocità, e si parla di frequenza di campionamento \( f_c\) e di tempo di campionamento \( T_c\), ovviamente vale: \( f_c = {1 \over T_C }\). Dovete pensare al campionamento come ad una videocamera che riprende una scena.
Maggiore è la “frequenza di scatto” (framing) maggiore è la fluidità del video (quindi il video rappresenta – approssima – sempre più la realtà) allo stesso modo maggiore è la frequenza di campionamento, cioè – il ripetere la misura, più fedele sarà il segnale digitale. Naturalmente frequenza di campionamento e tempo di campionamento sono inversamente proporzionali, quindi maggiore è la frequenza di campionamento, minore è il tempo di campionamenti, quindi più misure effettuo sul segnale nello stesso istante di tempo e più fine sarà la resa del segnale, parimenti minore è la frequenza di campionamento maggiore sara il tempo di misura e meno fine sarà il segnale misurato. Naturalmente qualcuno direbbe… perché non aumentare la frequenza di campionamento all’infinito di modo da eguagliare il versione analogica!
Teorema di Nyquist
Il motivo è che questo è impossibile! E questo è stato dimostrato un po di tempo fa nel 1950 circa da due ingegneri statunitensi: Nyquist e Shannon.
Il risultato cui giunsero, va sotto il nome di Teorema del campionamento o Teorema di Nyquist-Shannon, questo teorema sta a fondamento di tutta la teoria dell’informazione. Ed esprime quanto segue:
La frequenza di campionamento deve essere almeno il doppio della banda o della massima frequenza del segnale (frequenza di Nyquist)
Riassumendo: Campionamento: nella fase di campionamento il segnale viene misurato ad una frequenza detta di campionamento.
Quantizzazione in queta fase il dominio viene discretizzato, sostanzialmente ad ogni sotto-intervallo campionato viene
associato un valore costante. Codifica, nella fase di codifica si sceglie una risolizione in bit e l’intervallo dei valori è codificato.
(ad ogni valore discreto è associato un codice in bit).
$$ \LARGE \diamond $$
Naturalmente questo è solo l’inizio, tantissime cose le troverete presto nel corso di
Acustica ed Ingegneria del suono che sto preparando, che ancora è in fase di allestimento che a breve sarà disponibile! A presto