Wavelets

Prima di addentrarci nel mondo delle wavelets è necessario partire da oggetti piu’ familiari e dallo stato
dell’arte della strumentazione per quanto concerne i fenomeni ondulatori.

Serie di Fourier

Tutto ha inizio quando un fisico francese Joseph Baptiste Fourier fa una scoperta eccezionale! Lui scopre che le onde di tipo periodico si possono decomporre come accade con i vettori. Prendiamo ad esempio un vettore in \( \vec v \in \mathbb R^3\). Se muniamo \(\mathbb R^3\) di una terna di riferimento (quello che i matematici chiamano “base ortonormale di versori”) possiamo scrivere il nostro vettore \(\vec v\) nel modo seguente:

$$ \vec v = v_x\hat i + v_y \hat y + v_z\hat x $$ Possiamo addirittura, dimenticarci della base e considerare solo i numeri (le componenti)
disponendoli in una colonna: $$ \vec v = \begin{pmatrix} v_x \ v_y \ v_z \end{pmatrix} $$

Possiamo chiederci: chi sono le componenti? Che valore possiedono?

La risposta alla domanda non è difficile. Tutto dipende da un operazione fondamentale: il prodotto scalare.
Il prodotto scalare è il cuore della geometria, tecnicamente è una forma bilineare, simmetrica (alcuni autori preferiscono aggiungere
“definita positiva”) che soddisfa ad un gruppo di proprietà speciali:

$$ <\vec x,\vec y> \to \mathbb R $$

Sostanzialmente è un’applicazione che prende due vettori e ad essi associa un numero. Questo numero misura, per dirla alla buona, “il grado di somiglianza dei due vettori”
oppure “quanto essi sono affini” o ancora “come l’uno vede l’altro”. Se infatti il prodotto scalare è positivo \( <\vec x,\vec y> > 0 \) vuol dire che i vettori “si somigliano”,
hanno componenti in una direzione comune; se il prodotto scalare è negativo \( <\vec x,\vec y> < 0 \) vanno in direzioni opposte,
mentre quando il prodotto scalare è nullo \( <\vec x,\vec y> = 0 \) i vettori sono indipendenti – nessuno vede l’altro, sono invisibili.

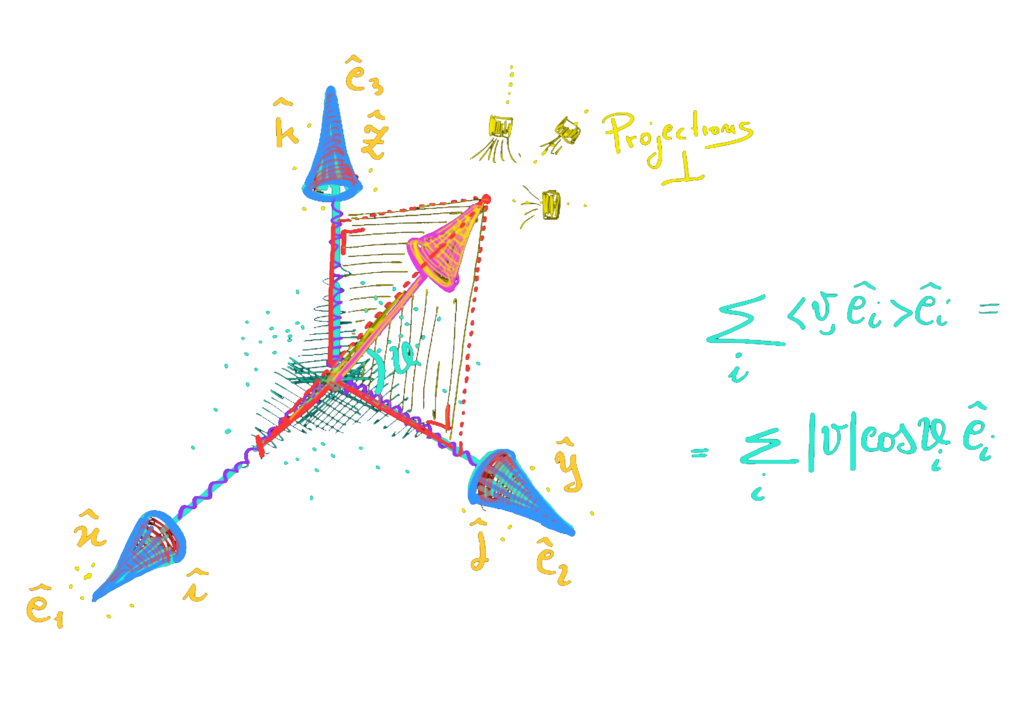
Quando abbiamo il prodotto scalare e la base ortonormale, è facile convincersi che le componenti, non sono altro che le proiezioni ortogonali
del vettore \( \vec v\) lungo le direzioni individuate dai versori della base:

$$ v_x = <\vec v,\hat i> \hspace{1cm} v_y = <\vec v,\hat j> $$ $$ \hspace{1cm} v_z = <\vec v,\hat k> $$

Quindi il nostro vettore puo scriversi come combinazione lineare (in un certo spazio vettoriale (V)) rispetto alla base attraverso questi coefficienti che prendono il nome di coefficienti di Fourier.

$$ \vec v = \sum_{i=1}^{dim(V)} <\vec v,\hat e_i>\hat e_i $$

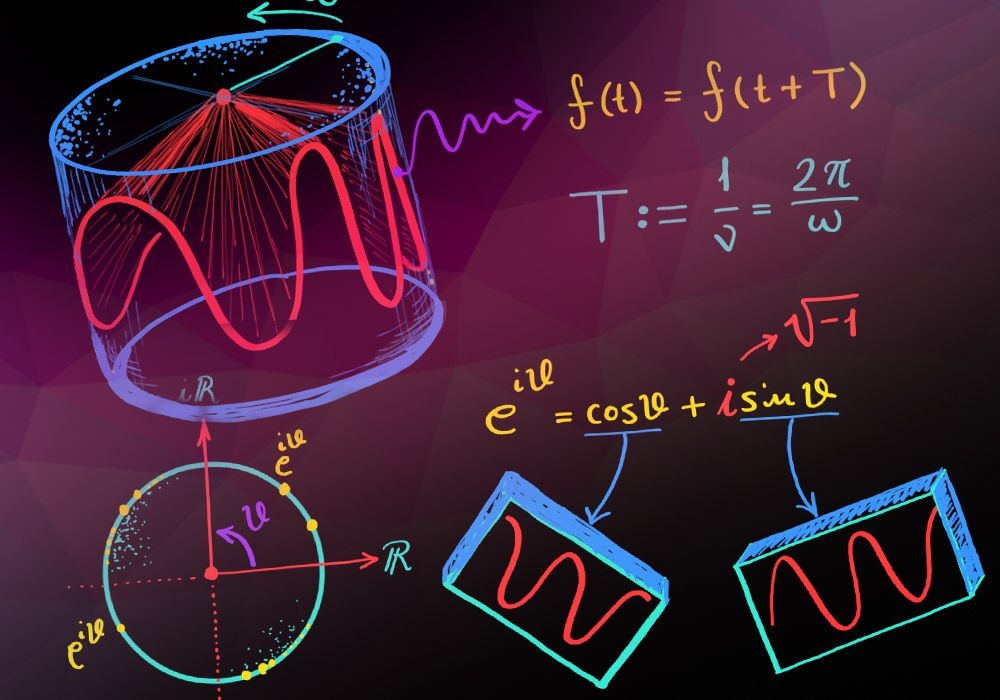
Consideriamo ora un’onda periodica di periodo \(T\), il periodo di un’onda è il tempo entro cui si manifesta tutta
l’informazione minimale dell’onda. Supponiamo per semplicità che sia \(T = 2\pi \). Ciò che Fourier scoprì è che anche una
funzione(segnale) \(f(t)\) periodico, cioè tale per cui \(f(t+T) = f(t)\) si può scrivere come combinazione lineare rispetto ad una certa
base in un certo spazio vettoriale astratto, ma quì c’è una differenza. Lo spazio ha dimensione infinita e gli elementi della base sono
infiniti e sono toni elementari con frequenze crescenti, ossia \(\sin(\omega t) \) e \(\cos(\omega t) \). Si ottiene una decomposizione di ogni funzione chiamata Serie di Fourier:

$$ f(t) = \alpha_0 + \sum_{i=1}^\infty \alpha_i \cos(\omega_i t) + \beta_i \sin(\omega_i t) $$

Resta da capire chi sono \(\alpha_0\), \(\alpha_i\) e \(\beta_i\).
Per fare questo bisogna capire che natura ha il prodotto scalare in questo spazio bizzarro.
Il settore della matematica che studia questi spazi a dimensione infinita è l’Analisi Funzionale e gli spazi sono i cosiddetti Spazi di Hilbert.
David Hilbert è stato uno dei piu’ grandi matematici tedeschi del ‘900, lo ricordiamo per la famosa lista dei 23 problemi che ha dato linfa agli sviluppi della matematica contemporanea,
molti dei problemi di Hilbert sono ancora aperti, ad esempio l’Ipotesi di Riemannn, la congettura di Goldbach ecc… Senza troppi tecnicismi, vi svelo subito chi è il famigerato prodotto scalare in questo spazio funzionale, eccolo quì:

$$ <f(t), g(t)> := {1\over 2\pi}\int_{-\infty}^{+\infty}f(t)\overline{g(t)}dt $$

Con molto stupore si tratta di un integrale! Qualcuno potrebbe storcere il naso, ma adesso sveliamo perché questa formula ha senso. Anzitutto la lineetta sulla \(g\) è l’operazione di coniugio o (coniugato). Questa operazione entra in scena quando lo spazio è complesso ed è necessaria per questioni di positività della metrica, ma non entriamo troppo in tecnicismi che altrimenti ci porterebbero fuori strada… Se lo spazio è reale la coniugazione sparisce perché per un numero reale \(x = \overline x\).

Come accade per lo spazio \(\mathbb R^n\) in cui il prodotto scalare è la somma dei prodotti delle componenti corrispondenti dei due vettori, qui’ il discorso è identico,
ma ora siccome lo spazio è infinito-dimensionale la somma va sostituita con un integrale, mentre le componenti sono le immagini delle funzioni nella variabile indipendente, es. \(t\).

E’ facile convincersi, che i coefficienti

dello sviluppo di Fourier sono:

$$ \begin{cases} \alpha_0 = {1 \over 2\pi} \int_{-\pi}^{pi}f(t)dt \\
\alpha_i = {1 \over \pi} \int_{-\pi}^{\pi}f(t)\cos(\omega_i t)dt \\
\beta_i = {1 \over \pi} \int_{-\pi}^{\pi}f(t)\sin(\omega_i t)dt \\
\end{cases} $$

$$ \diamond $$

$$ \diamond $$

Trasformata di Fourier

i chiediamo ora cosa succede se la nostra funzione(segnale) (f(t)) non fosse periodica e si estendesse su tutto ( \mathbb R). Quì entra in scena la Trasformata di Fourier!

Il significato di questa definizione è profondo e meriterebbe una discussione piu ampia, ma possiamo interpretarlo con l’idea di prodotto scalare molto facilmente.
In effetti non è difficile accorgersi che si tratta effettivamente di un prodotto scalare tra la \(f(t)\), e l’oggetto \( (e^{-i\omega t} ) \).

Questo oggetto è l’elemento oscillante elementare, è un fasore rotante e racchiude in forma complessa il contenuto in frequenza di un tono elementare.

Se ci ricordiamo che il prodotto scalare è una sorta di misura del gradi di somiglianza di due vettori, allora la Trasformata di Fourier ci dice quanto una certa frequenza è presente nella nostra funzione.
In sostanza ci restituisce lo spettro di tutte le frequenze (o meglio delle pulsazioni, ma non fa molta differenza visto che \( \omega = 2\pi \nu) \) presenti nel segnale e per ciascuna di esse naturalmente ci da
la relativa l’intensità.

Ora quì sorge un problema! Si nota che la nostra trasformata ha perso dal punto di vista analitico la dipendenza dal tempo! E’ una funzione della sola \( \omega\).
Siamo passati da una risoluzione infinita nel tempo e nulla in frequenza ad una risoluzione infinita nella frequenza e nulla nel tempo.
Questo potrebbe sembrare un gioco per tediare qualcuno, ma ora vi mostro cosa si nasconde dietro questo discorso…

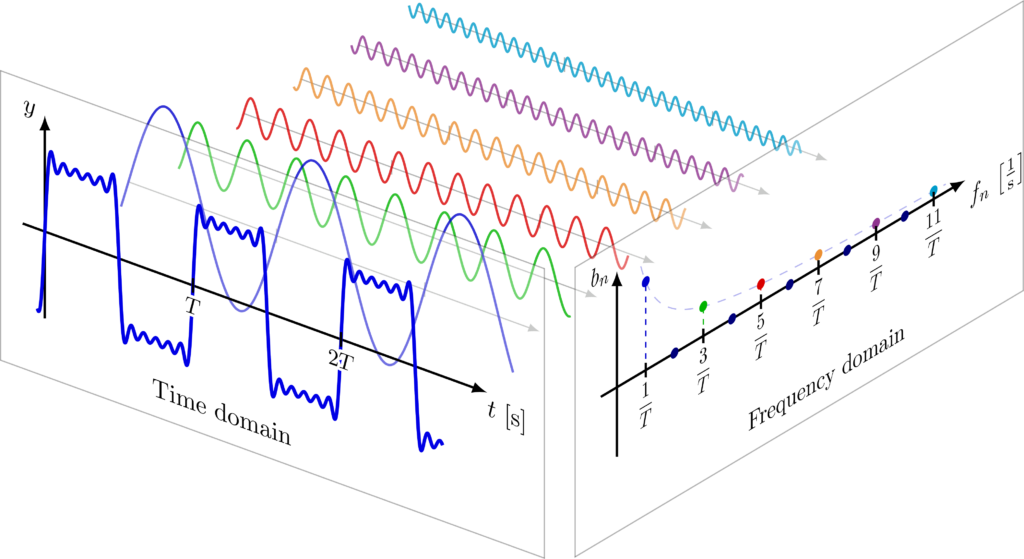
Supponiamo di trovarci con la nostra auto davanti ad un semaforo (oppure, per i musicisti, di trovarci in una sala musicale con un pianoforte). Ora all’inizio, stranamente, il nostro semaforo ha tutte le luci accese – forse è difettoso – e noi per passare il tempo magari mentre qualcuno viene a ripararlo prendiamo il nostro analizzatore e calcoliamo la Trasformata di Fourier del semaforo… nel caso dei musicisti, (suoniamo un accordo, delle note in contemporanea e con un microfono ed un analizzatore, calcoliamo la Trasformata di Fourier dell’accordo musicale), “per abbreviare ora invece di scrivere sempre Trasformata di Fourier”, scriverò semplicemente: FT.

Che cosa vediamo? Come sarà il nostro spettro?

Avrà dei picchi in corrispondenza delle frequenze dei colori (rosso, giallo, verde), nel caso del semaforo e delle fondamentali nel caso dell’accordo. Giusto! Bene…

Ora, finalmente il semaforo funziona e prima di partire di nuovo calcoliamo la FT questa volta però mentre i colori si estrinsecano nel
tempo prima rosso poi giallo e poi verde (nel caso del musicista chiediamo di suonare delle note da un pentagramma nel tempo).
Come sarà lo spettro questa volta? Risposta: uguale a prima!

Questò è un problema. Perchè la FT non distingue i due casi! Essa è cieca al tempo.

I segnali generati da un semaforo con tutte le luci accese o da un accordo musicale in cui tutte le
frequenze sono presenti in tutti gli istanti di tempo, sono chiamati segnali stazionari, mentre quelli in cui la frequenza varia nel tempo,
sono chiamati segnali non stazionari. La FT non è adatta allo studio dei segnali non stazionari. $$ $$

La Trasformata di Fourier a tempo breve: STFT

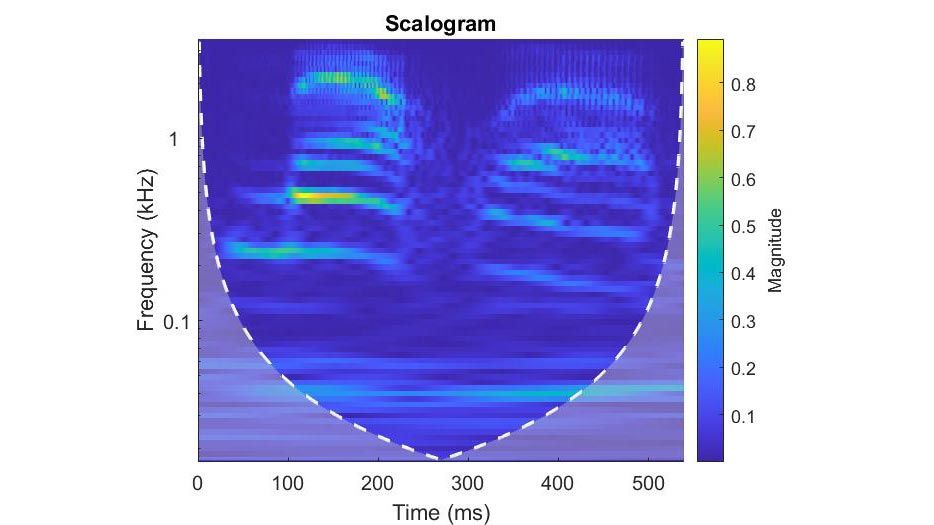
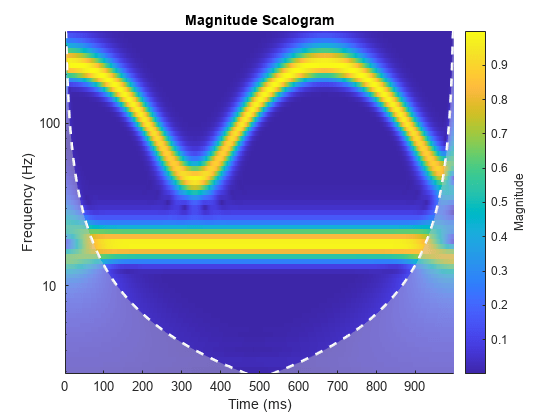
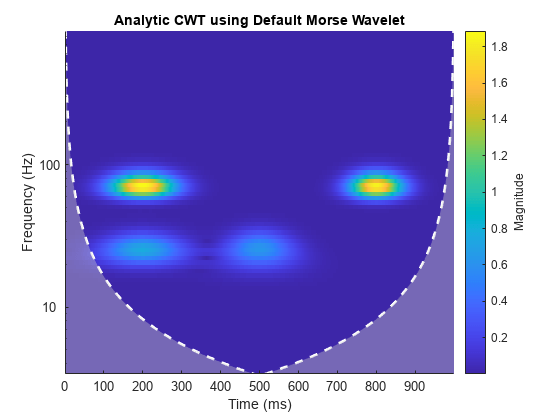
Un modo per superare tale difficoltà, consiste nel fare l’analisi di Fourier riducendo la risoluzione temporale così da avere piu’
informazioni in frequenza. Nel 1946 Dennis Gabor, un ingegnere elettrico ungherese ebbe l’idea di costruire una versione speciale della
trasformata in cui procede all’analisi per porzioni attraverso una finestra temporale che riduce l’azione della FT a brevi intervalli temporali, la cosiddetta STFT (Short Time Fourier Transform):

Moltiplicare il segnale per \(g(t-\tau)\) equivale in effetti a selezionarne una porzione il cui supporto coincide con l’intervallo di traslazione \(\tau\).
In sostanza si trasla e si moltiplica come avviene con il prodotto di convoluzione. Quello che otteniamo è il contenuto in frequenza in ogni finestra, quindi sappiamo meglio
in quale intervallo temporale sono presenti certe frequenze.

Questo limite di dettaglio, non è un problema “ingegneristico”, ma è proprio un limite fisico, ossia una rappresentazione del Principio di indeterminazione di Heisemberg, il quale afferma (nel nostro contesto)
che non è possibile conoscere con esattezza contemporaneamente sia il valore temporale che in frequenza. Se “mettiamo a fuoco, facciamo uno zoom sul tempo”
non sappiamo cosa accade in frequenza e viceversa, le due quantità sono inversamente proporzionali, come espresso da questa diseguaglianza.

$$ \sigma_t \sigma_\omega \geq {1\over 2} $$

Le due quantità non possono essere “piccole entrambe”, perché se fosse “troppo piccola” la \(\sigma_t\), siccome il prodotto deve essere maggiore di \({1\over 2}\)
allora \(\sigma_\omega\) deve essere “grande” affinché sia valida la disuguaglianza, e viceversa.

Il limite di questa analisi è ora, legato fortemente alla scelta della finestra, che rimane comunque “fissa”, infatti la scelta dell’incertezza
\(\Delta t \) sull’asse dei tempi, stabilisce per tutto il procedimento di analisi anche l’incertezza \(\Delta_\omega\) sull’asse delle frequenze,
ciò appare piu’ evidente con i cosiddetti Box di Heisemberg:

Gabor fece un altro passo avanti, introducendo i cosiddetti Atomi di Gabor e quindi la sua Trasformata di Gabor, dove la differenza è la scelta della finestra, che è di tipo gaussiano:
Inoltre Gabor capì che modulando opportunamente i suoi atomi (le finestre gaussiane) e traslandole poteva modificare l’incertezza “tempo-frequenza”
durante l’analisi spettrale, ma fu un altro francese Morlét a fare compiere il passo decisivo…

La Trasformata Wavelet ed il Regno delle ondine

Morlét affronto la questione in modo leggermente differente: invece di modulare le gaussiane, perché non cerchiamo delle funzioni speciali in modo che la dilatazione provochi indirettamente anche una modulazione. Questa idea porto alla scoperta delle cosiddette wavelet, ondelette oppure in italiano ondicine (ondine), ondicelle…

Attraverso le ondine si ottiene uno strumento il cui potere è assoluto: La Trasformata Wavelet, un vero e proprio “microscopio matematico”.

La proprietà speciale di una ondina è che adesso a differenza di quello che succede con la STFT la finestra ha ampiezza del supporto variabile durante l’analisi.
Nell’integrale compare un nuovo oggetto \( \psi^\xi_\zeta = {1\over\sqrt \xi}\psi\left(t-\zeta \over \xi\right) \) chiamato “wavelet madre”. Madre,
perché da essa, attraverso la modifica dei parametri nascono tutte le “ondine figlie”.

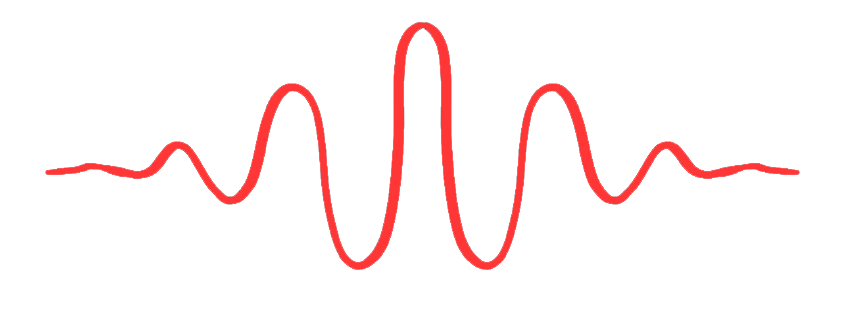
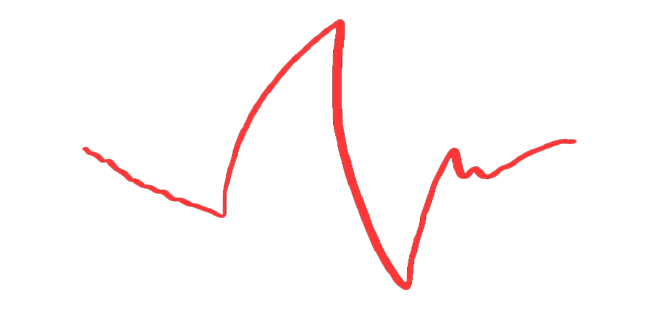
Ma che cos’è una wavelet matematicamente parlando? Non è solo una funzione ma una famiglia di funzioni che soddisfano ad alcuni requisiti:
C’è uno “zoo” di ondine, ciascuna con applicazioni specifiche…

Una funzione per essere una ondina deve soddisfare a due requisiti fondamentali:

$$ $$

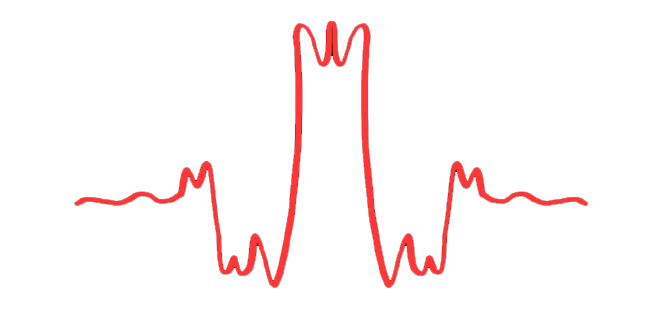
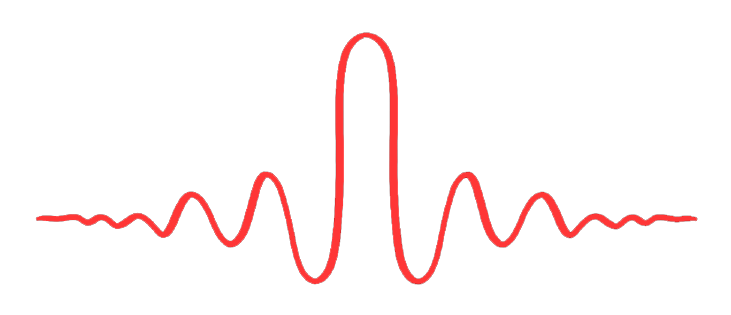
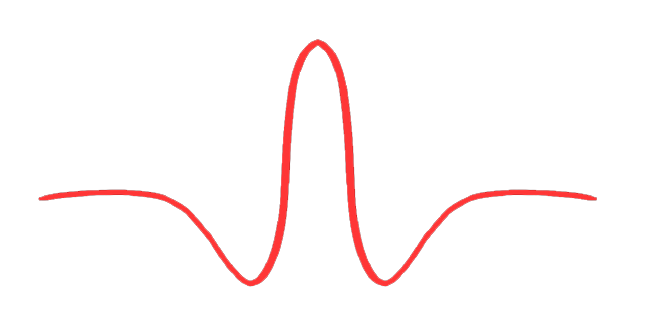
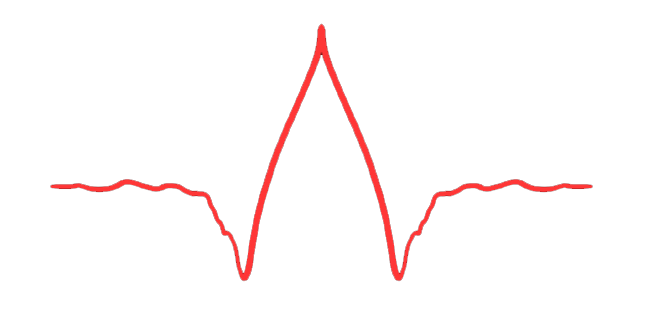
E’ questo che rende l’ondina localizzata nel tempo. Ad esempio, la Wavelet di Morlet, si ottiene attraverso un esponenziale complesso moltiplicato per una finestra gaussiana, questa wavelet ha delle peculiarità sia in campo acustico che visivo:

$$ \psi(t) = K(e^{i\sigma t}-k_\sigma)e^{-{t^2 \over 2}} $$

a presto per per approfondimenti…

giux

• [1]: A volte la coniugazione è indicata con il simbolo \(*\), per cui si avrebbe: \( <f(t), g(t)> := {1\over 2\pi}\int_{-\infty}^{+\infty}f(t)g(t)^*dt \)
• [2]: Nelle applicazioni non matematiche (Ingegneria, Elettronica, Segnali) Si usa scrivere al posto di \(i\) per l’unità immaginaria \(j\) per non confondersi con l’intensità di corrente elettrica e quindi si scrive \(e^{-j\omega t} \)