Pierre-Simon Laplace nasce il 23 marzo del 1749 a Beaumont-eu-Auge, in un piccolo paesino della Normandia in Francia vicino alla foce del fiume Senna tra orchidee, prati e meli.
Considerando le origini nessuno si sarebbe mai aspettato che diventasse uno dei più grandi scienziati del mondo…
L’infanzia e la matematica
Apprese le lettere, le 4 operazioni dallo Zio Louis, “l’abate Laplace” un sacerdote cattolico, che pare abbia inculcato alcuni rudimenti matematici nel piccolo Laplace durante la sua infanzia “quando la mente apprende rapidamente“. La famiglia decise che avrebbe intrapreso una carriera ecclesiastica, letteraria e teologica. Frequentò fino ai 17 anni un collegio benedettino e poi si iscrisse all’università per completare gli studi. Ma proprio nel 1768 accadde nella mente di Laplace qualcosa di insolito…. abbandono gli studi misteriosamente senza completare la laurea. Era stato folgorato dalla matematica – nella stessa università aveva seguito dei corsi di matematica superiore ed aveva scoperto il suo talento per la scienza.
Si trasferì a Parigi, all’ora, la capitale dell’illuminismo, la città della luce contro la volontà del padre, e portava con se una lettera di raccomandazione dei suoi professori; si guadagno l’attenzione dell’allora più illustre matematico di Parigi Jean Le Rond D’Alembert, il quale non diede credito alla raccomandazione, cosi Laplace gli scrisse direttamente, spiegandogli le sue idee sulla meccanica e sull’universo. D’Alembert rimase stupito del giovane ventenne e gli procurò un posto come professore di matematica all’accademia militare di Parigi.
Ma il sogno più grande era entrare nell’Academia delle Scienze di Parigi, il massimo prestigio per uno scienziato del tempo in Francia. Passò ore con D’Alembert a studiare gli scritti di Eulero, Newton, Leibnitz – apprese la meccanica analitica, l’analisi superiore, la geometria e le equazioni differenziali dove era esperto nella risoluzione.
Equazioni Differenziali
Una equazione differenziale è una equazione in cui l’incognita non è un numero ma una funzione. Le equazioni differenziali sono lo strumento più importante per un fisico, descrivono le leggi naturali in un modo assolutamente “vicino alla realtà”. è celebre la citazione:
“L’universo è un’equazione differenziale”
H. Poincaré
Esistono sostanzialmente due grandi classi di equazioni differenziali: quelle lineari in cui vale la sovrapposizione e quelle non lineari piu complesse, la cui risoluzione necessita di metodi di approssimazione – l’esempio piu familiare a molti è l’equazione della dinamica di Newton:
$$ \vec F = m\vec a $$
Che afferma che “La forza (interazione) di un corpo è pari al prodotto della sua massa per la sua accelerazione“. In questa relazione l’incognita è proprio \(\vec a\), che non è un numero ma una funzione, o per essere precisi un rapporto di variazioni: \( \vec F = m {d^2x \over dt^2} \).
Finalmente nel 1773 il sogno ambito divenne realtà, Laplace entrava nell’Accademia delle Scienze ed incominciava una nuova avventura.
Il Laplaciano
E’ famoso tra i fisici l’operatore di Laplace o “Laplaciano“. Una versione multidimensionale della derivata seconda: Il laplaciano è definito nel modo seguente:
$$ \nabla^2\Phi = \Delta\Phi = {\partial^2\Phi \over \partial x^2} + {\partial^2\Phi \over \partial y^2} + {\partial^2\Phi \over \partial z^2} $$
$${\large \mathrm{Lap}(\Phi) = \nabla^2\Phi = \sum_{i=1}^n{\partial^2\Phi \over \partial x_i^2} }$$
Si incontra spesso in elettromagnetismo, ma anche in meccanica analitica ed in fluidodinamica, si tratta di uno degli operatori fondamentali del calcolo differenziale.
$$ \diamond$$
Il sistema del mondo
Siamo nel decennio del 1770, Laplace inizia un viaggio verso le meraviglie dell’universo. All’epoca vi erano una serie di grandi domande alle quali non vi era risposta “perché i pianeti orbitano senza cadere?”, “qual è la forma della terra?”, “quali sono le traiettorie delle comete?” La sua mente iniziò a viaggiare, presto comincio a prendere forma il suo grande contributo alla scienza dell’universo:
Vortici e gravitazione
Isaac Newton aveva definito nei suoi Principia, la legge di gravitazione universale che descriveva i moti dei pianeti attorno al sole e spiegava perché le cose cadono a terra, le maree, le comete ecc… anche un altro scienziato Cartesio aveva dato interpretazioni in merito (come ad es: l’idea dei vortici), ma le sue idee erano state offuscate dal grande Newton. Tuttavia Laplace si accorse di un fatto singolare: sia le concezioni di Newton che quelle di Cartesio erano descrizioni di tipo meccanicistico.
Secondo i cartesiani essendo lo spazio pieno di materia e/o fluidi, gli spostamenti si manifestano sotto forma di “vortici o mulinelli“ non in linea retta – cosi si spiegherebbe il fatto che i pianeti ruotano attorno al sole; perché trascinati dal moto di turbine di materia circostante, mentre secondo i newtoniani tutto dipendeva dalla presenza del sole, ed i pianeti ne subivano l’influsso – “Lo stesso Newton d’altronde non era a conoscenza di cosa fosse l’ente misterioso che produceva questa “forza gravitazionale“, bisognerà attendere l’ingresso di Albert Einstein nel 1915 con la sua Relatività Generale
Laplace era rimasto affascinato dalla legge di gravitazione universale di Newton che affermava una cosa semplice ma profonda: la forza con cui si attraggono due corpi è proporzionale al prodotto delle loro masse ed inversamente proporzionale al quadrato della loro distanza.
$$ \vec{F_G} = \mathrm G{Mm \over d^2}\vec{r} $$
Inizio a nascere la visione di un universo determinista e stabile regolato da un unico principio.

La forma della terra
La prima questione che affrontò Laplace era indagare sulla forma della terra. Già i greci avevano attribuito alla terra una forma sferica, Copernico ne aveva discusso il movimento, ma c’era una questione che metteva in competizione le idee di Cartesiane e quelle Newtoniane – ossia il fatto che durante il suo moto la terra dovrebbe apparire non perfettamente sferica ma schiacciata dai poli – come una zucca (Terra Newtoniana), o come un melone (Terra Cartesiana), schiacciata lungo l’equatore.
Laplace diede credito alla prima versione che poi fu confermata misurando (i gradi di meridiani dopo una lunga disputa tra le fazioni).
L’orbita delle comete
Quante volte guardando al cielo avete visto una cometa ed espresso un desiderio? Le comete hanno sempre affascinato tutti. All’inizio si pensava si trattasse di fenomeni atmosferici, ma presto si capi essere astri e si tento di spiegarne il moto , questo sarebbe stato un punto avantaggio di newton , se infatti avessero attraversato il sistema solare senza essere trascinate dalla corrente del vortice, ciò avrebbe significato la non esistenza dei vortici. Newton nei principia aveva ipotizzato che le comete avrebbero descritto traiettorie coniche (parabola ellisse iperbole circonferenza)
Se avesse descritto traiettorie circolari o ellittiche sarebbe riapparsa ad intervalli regolari, se avesse tracciato parabola o iperbole dopo essere apparsa sarebbe scomparso nell’universo oscuro
Le anomalie secolari di Giove e Saturno
C’erano alcune anomalia ancora: secondo i principia se il sole gravita verso i pianeti a, che i pianeti gravitano verso il sole, tutti gravitano verso tutti. Newton studio cosa accadeva prendendo il sole ed un pianeta: questo era relazionato al problema matematico degli n corpi: Eulero risolse per n = 2 , e la soluzione era che si muovevano lungo sezioni coniche.
Passando a tre corpi i matematici si trovarono ad affrontare un problema estremamente complesso
Come aveva constatato Halley un secolo prima Giove e Saturno apparivano bizzarri: il primo accelerava mentre Saturno rallentava, questo avrebbe provocato il seguente scenario: “Giove si sarebbe scontrato con il sole” “Saturno sarebbe si sarebbe dileguato nell’universo“
Laplace trovo la soluzione nell’opera “Sulle disuguaglianze secolari dei pianeti e satelliti e Teoria di Giove e Sturno”
Laplace trovo un’equazione che gli rivelo una sorpresa inaspettata”, una proprietà speciale del nostro sistema solare: “la costanza dei moti medi dei pianeti”
Se ci fosse solo un pianeta questo seguirebbe un’orbita normale ellittica attorno al sole, ma siccome ce ne sono altri l’orbita si ottiene partendo dall’orbita ellittica e aggiungendo una “piccola perturbazione”
Ora il sole ha una massa del 98,87% di tutto il sistema solare, quindi le orbite dei pianeti sono pressoché ellittiche
Giove possiede il 70% della massa planetaria e per questo influisce principalmente sul resto dei pianeti, se prendiamo il sistema dei tre pianeti Giove, sole saturno, ci sarebbero forti perturbazioni tra Giove e Saturno e nessuna sul sole ecc..
Ma Laplace non si fermo e studio la luna , scrisse un’altra memoria “Sull’ equazione secolare della luna” e spiego un fenomeno strano “la librazione lunare“.
Laplace, la Rivoluzione Francese e il Sistema Metrico Decimale
Il 1789 è l’anno della Rivoluzione Francese. I disordini nel regno erano oramai fuori controllo ed in quello stesso 1789 vi fu la Presa della Bastiglia a Parigi e la fuga di Luigi XIV e di sua moglie che vennero catturati a Varelles. I matematici vissero quei momenti in un misto di paura e speranza. Laplace da opportunista qual era cavalco l’onda della rivoluzione per accrescere i suoi obbiettivi: diventare il difensore piu’ importante della scienza francese.
Nel 1791 era entrato nell0ufficio delle cnsulenze di arti emestieri a visionare brevetti ed invenzioni, ma presto nel 1793/94 (siamo nel periodo del terrore) Laplace fu defenestrato e ltri scienziati vennero ghigliottinati, tra cui Lavoisier (capo degli esattori delle imposte odiato dal popolo) Condorcet ed altri. Laplace fuggi da Parigi in una piccola città a 50Km Melun e solo alla fine del Terrore ritornò con n voluminoso manoscritto sottobraccio.
Pesi e Misure
L’infinita varietà di misure disponibili in Francia sfuggiva ad ogni comprensione circa 250000 misure diverse, anche di famiglia in famiglia usavano sistemi diversi di misura.
In quel perioodo si era formata una commissione sui pesi e misure presieduta da LLagarnge di cui era membro Laplace, che pare abbia suggerito lui quello che oggi e il sistema metrico decimale con il metro, il centimntro, i lidri i grammi l’area ecc.. Il sistema metrico decimale venne istituito il 7 aprile del 1795. LAplace fu impegnato nel trovare una efiniizone esatta del metro (oggi il metro non viene piu definito come la decimilionesima parte del quadrante di un meridiano terrestre, ma come la lunghezza che percorre la luce nel vuoto in \( {1 \over 299458792 }{m \over s} \). Infine partecipa come fondatore dell’ Ecole -Politencique e della Scuola Normale, esamina un giovane aspirante che poi diventerà Napoleone Bonaparte e sarà cancelliere del senato.
L’Universo di Laplace
Le due opere monumentali di Laplace, “L’Esposizione del sistema del mondo” ed il “Trattato di Meccanica Celeste” pare siano state scritte da Laplace durante la sua fuga dal Terrore a Melun. Nel sistema del mondo Laplace descrive i chiave illuministica il sistema solare in uno splendido paesaggio ” se durante una notte limpida osserviamo lo spettacolo del cielo, notiamo c he cambia in continuazione gli astri i pianeti erranti e vagabondi (Mercurio Venere, Marte Giove e Saturno) visibili ad occhio nudo, parla anche elle stelle e descrive quella luce bianca che circonda il cielo come fosse una cintura (la Via lattea), in sintesi Laplace elenca tutti gli oggetti astronomici dai piu’ grandi ai piu’ piccoli
L’ipotesi nebulare e l’origine del sistema solare
Nel 1976 Laplace fece un’ipotesi sulle origini dell’Universo. Nello spazio di poche pagine Laplace si avventuro nel terreno della cosmologia. La sua ipotesi si rifaceva ad un concetto di Kant (da qui Ipotesi di Kant-Laplace) di nebulosa primordiale, anche se lui non era a conoscenza dell’opera di Kant ma era a conoscenza di u altra congettura del conte di Buffon secondo cui l’universo si sarebbe formato da un impatto con il sole ed i frammenti sarebbero diventati i pianeti dopo essersi raffreddati.
Secondo Laplace il sistema solare si sarebbe invece formato da una nebulosa primitiva solare che, formando degli anelli e pò dei grumi di asti si sarebbero formati i pianeti.
Nel suo trattato di meccanica celeste opera in 5 volumi Laplace racconta con il linguaggio matematico l’astronomia , dove presentava in forma analitica molti dei risultati del sistema del mondo
La trasformata di Laplace
La trasformata di Laplace è uno degli strumenti piu’ utilizzati nella nella risoluzione delle equazioni differenziali. Pare Laplace l’abbi scoperta nel 1782, ma solo Oliver Heaviside l’ha resa nota per come oggi la conosciamo.
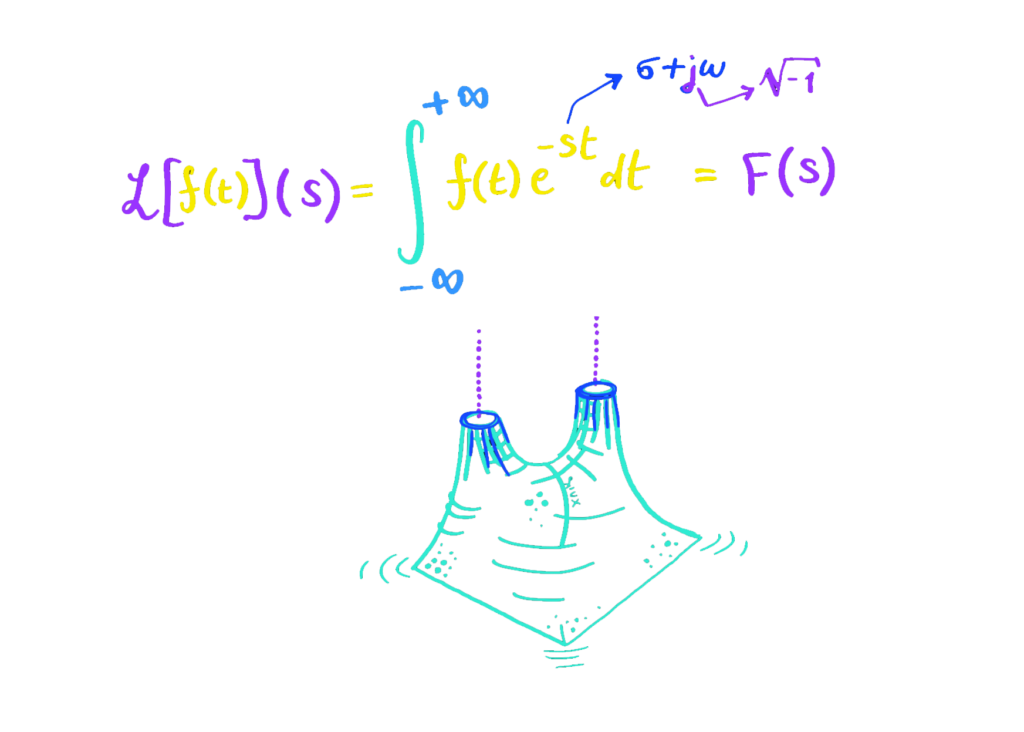
L’eredità del Newton francese
Laplace ci ha lasciato una grande eredità di strumenti e concetti: L’equazione di Laplace, il metodo per lo sviluppo dei determinanti, le basi dell’inferenza statistica, La Trasformata di Laplace, il sistema metrico decimale la scuola laplaciana e le sue opere straordinarie e cc
Probabilità e determinismo
Verso la fine del ‘700, Laplace si occuperà di probabilità. Fino ad allora la probabilità era una disciplina basata sull’algebra, non elevata al rango delle scienze come la geometria o la meccanica; molti matematici la associavano ad un puro divertimento ricreativo e spesso speculativo con cui divertirsi giocando con urne e mazzi di carte. Laplace fece un lavoro straordinario unendo l’analisi matematica alla probabilità, opera che si concluderà nel 1812 con “La teoria analitica delle probabilità” ed il “saggio filosofico” due anni dopo in cui Laplace riscriverà in una nuova formulazione il teorema del limite centrale, la formula di Bayes e darà una definizione “La regola di Laplace” che afferma che
“La probabilità di un successo è data dal numero di casi favorevoli diviso il numero di casi possibili”
Pierre-Simon Laplace e stato uno dei piu’ grandi newtoniani, piu’ che innovatore fu un difensore di Newton non fu un rivoluzionario per che non mise in dubbio la struttura ereditata da newton, l’unica cosa che non riuscì a comprendere -essendo lui ateo determinista – era perché il suo grande mentore si era affidato ad un universo divino ed ad affidare a Dio un ruolo centrale nel sistema del mondo
un sabato 3 marzo 1827 due giorni prima di spirare Laplace ci lascio con le sue ultime parole:
“Ciò che conosciamo è pochissimo, quello che ignoriamo è immenso… L’uomo può solo inseguire chimere”
Pierre-Simon Laplace