Home » Matematica
16 Posts

Matematica

Il Tensore di Ricci e la geometria della gravità
Categories

Il Tensore di RICCI demistificato: Il Cuore della Relatività Generale

  • Posted byby GIUX
  • 5 min
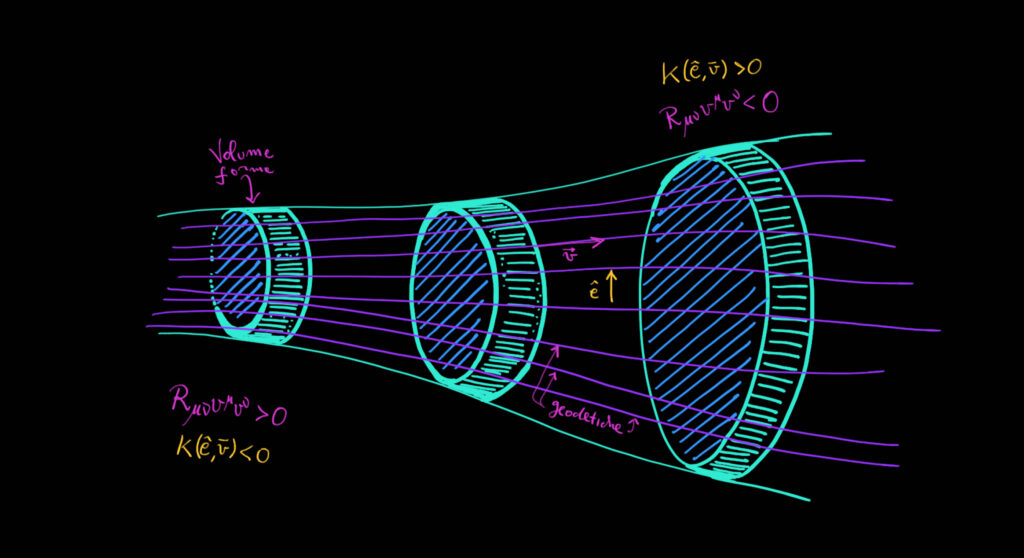
Il Tensore di Ricci, noto anche come Tensore di Ricci-Curbastro o più semplicemente "Tensore di Ricci," è un oggetto matematico fondamentale utilizzato in fisica teorica, in particolare nella teoria della relatività generale di Albert Einstein. Questo tensore è una componente chiave delle equazioni di campo di Einstein, che descrivono come la gravità si manifesta nello spazio-tempo. In questo breve articolo scopriremo di cosa si tratta...
Pigreco irrazionale
Categories

L’irrazionalità di π

Sebbene la prima dimostrazione dell’irrazionalità di π risalga agli anni 1760 (Lambert, un amico di Eulero), la dimostrazione può semplice oggi nota `e stata scoperta solo in tempi sorprendentemente recenti: nel 2010 (Zhou, Markov). Essa sfrutta solo l’integrazione per parti ed `e in teoria accessibile anche a un bravo studente delle superiori. La ho trovata sfogliando l’ottimo Elementary Analysis di Ross e la riporto qui (spezzettata in 10 punti) cercando di essere il piu' semplice e dettagliato possibile. Spero che il lettore apprezzi la bellezza del risultato, oltre alla perseveranza e alla creatività di Zhou e Markov, che ci hanno regalato questa perla.
Categories

L’Universo di Laplace

  • Posted byby GIUX
  • 8 min
Pierre-Simon Laplace nasce il 23 marzo del 1749 a Beaumont-eu-Auge, in un piccolo paesino della Normandia in Francia vicino alla foce del fiume Senna tra orchidee, prati e meli. Considerando le origini nessuno si sarebbe mai aspettato che diventasse uno dei più grandi scienziati del mondo...
Carl Friedrich GAuss
Categories

Gauss e il burbero maestro

  • Posted byby GIUX
  • 2 min
Vi racconto un aneddoto di uno dei più grandi matematici mai esistiti. Carl Friedrich Gauss: Astronomo, Fisico, Matematico, Topologo e chi più ne ha più ne metta… è stato soprannominato il Principe dei Matematici per le sue innumerevoli scoperte ed i suoi enormi contributi in quasi tutte le branche delle scienze. Già da piccolo mostrava una forte attitudine alla matematica… seguitemi, ci spostiamo nel 1785 a Brunswick.
Il paradosso dei due bambini
Categories

Il paradosso dei due bambini

Venne proposto da Martin Gardner sulle pagine del Scientific American. La formulazione è la seguente: Il signor Smith ha due bambini. Almeno uno dei due è un maschio. Qual è la probabilità che entrambi i bambini siano maschi? Ad una risposta contraria alla "logica comune"

Iscriviti per rimanere aggiornato

Euler's Gamma

Gaussian

Euler's angles

Sea shell

Riemann surface

Calabi-Yau Manifold